SECTION 6.5PASCAL’S TRIANGLE

© Copyright all rights reserved to Homework depot: www.BCMath.ca

BLAISE PASCALE AND PASCAL’S TRIANGLE

Blaise Pascal (June 19, 1623 – August 19, 1662) was a Frenchmathematician, physicist, and religious philosopher

He used the triangle to solve problems in probability theory.

Numbers used in Pascal’s triangle was discovered by manymathematicians before him but with different applications

The earliest explicit depictions of the triangle occur in the 10thcentury in commentaries on the Chandas Shastra (India)

In Iran, it is known as "Khayyam triangle” (1048-1131); , finding nthroots of a binomial expansion (section 6.6)

In China, it is known as “Yang Hui'striangle"(1238-1298)

In Italy, they call it "Tartaglia's triangle", used insolving cubic polynomials(1500-1577)

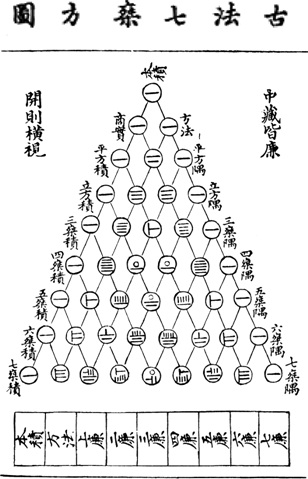
© Copyright all rights reserved to Homework depot: www.BCMath.ca

PASCAL’S TRIANGLE

1

Begin with three 1’s on the top

Each number is the sum of thevalues directly above

1

1

1

2

1

1

3

3

1

1

4

6

4

1

1

5

10

10

5

1

1

6

15

20

15

6

1

1

7

21

35

35

21

7

1

1

8

28

56

70

56

28

8

1

1

9

36

84

126

126

84

36

9

1

1

10

45

120

210

252

210

120

45

10

1

© Copyright all rights reserved to Homework depot: www.BCMath.ca

PASCAL’S TRIANGLE WITH COMBINATORICS

Each row corresponds

with the value of “n”

Each diagonal columncorresponds with thevalue of “r”, beginningwith r = 0

Begin with  n = 0 atthe top

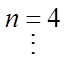
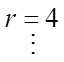
Note: The nth row will have with have “n+1” columns

Ie: when n=5, there will be 6 diagonal columns

© Copyright all rights reserved to Homework depot: www.BCMath.ca

SYMMETRICAL PATTERN:

There is a symmetrical pattern in Pascal’s triangle

Opposite sides of the triangle are equal

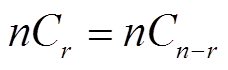
General formula forSymmetrical Pattern:

© Copyright all rights reserved to Homework depot: www.BCMath.ca

RECURSIVE PATTERN:

Each term is the sum of the two terms directly above

If there is only one term above, then they will be equal

General formula forRecursive Pattern:

© Copyright all rights reserved to Homework depot: www.BCMath.ca

PATHWAY PROBLEMS:

Ex: Using Pascal’s Triangle, find the number of pathways from Ato B, if you can only go right or down.

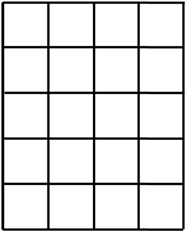
A

B

A

B

1

1

1

1

2

1

1

3

3

1

1

4

6

4

1

1

5

10

10

5

6

15

20

15

21

35

35

56

70

126

1

1

1

1

2

1

1

3

3

1

4

6

4

1

10

10

5

10

20

15

10

30

35

15

40

65

50

15

105

115

65

220

180

220

400

520

400

1020

© Copyright all rights reserved to Homework depot: www.BCMath.ca

EX: IN THE GAME OF CHECKERS, YOU CAN ONLY GO FORWARD BYMOVING DIAGONALLY TO THE LEFT OR RIGHT.  WITH THEFOLLOWING CHECKER, HOW MANY WAYS ARE THERE TO REACHTHE OTHER SIDE?

1

1

1

2

1

1

3

3

1

4

6

4

1

4

10

10

5

14

20

15

5

14

34

35

20

The total number of ways toreach the other side will be:

© Copyright all rights reserved to Homework depot: www.BCMath.ca

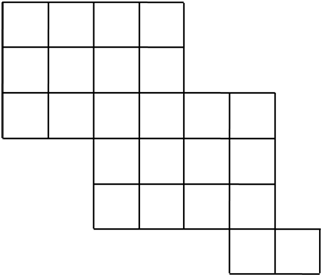
CHALLENGE: JACK CAN ONLY TRAVEL EAST OR SOUTH TOGET TO WORK.  GIVEN THE FOLLOWING OBSTACLES, HOWMANY PATHWAYS ARE THERE FROM “A” TO “B”?

Obstacles:

Flood

Accident

A

B

Nuclear Bomb

1

1

2

1

3

1

1

3

6

1

4

10

4

10

20

1

5

1

1

6

1

7

6

13

20

26

39

1

10

20

46

85

1

1

11

2

11

13

24

31

55

77

162

132

294

© Copyright all rights reserved to Homework depot: www.BCMath.ca

HOMEWORK:

P384 #1 – 6, 10 – 13, 15 – 20

© Copyright all rights reserved to Homework depot: www.BCMath.ca

CHALLENGE: SOLVE FOR “N”

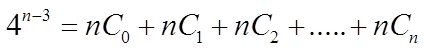
For each row in Pascal’s triangle,

the sum of all the coefficients isequal 2n

© Copyright all rights reserved to Homework depot: www.BCMath.ca